Darlington and Sziklai pair
Cascading of two bipolar transistors is commonly used to create a virtual transistor with high current gain. The transistors can be of the same polarity (Darlington, Fig. 1) or of the opposite polarities. The later configuration is called "Composite Darlington" or Sziklai pair (Fig. 2), as depicted below in a common emitter configuration.
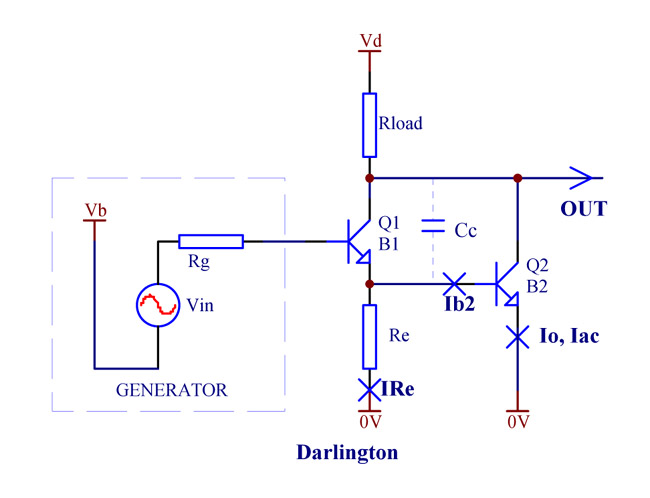
Fig. 1
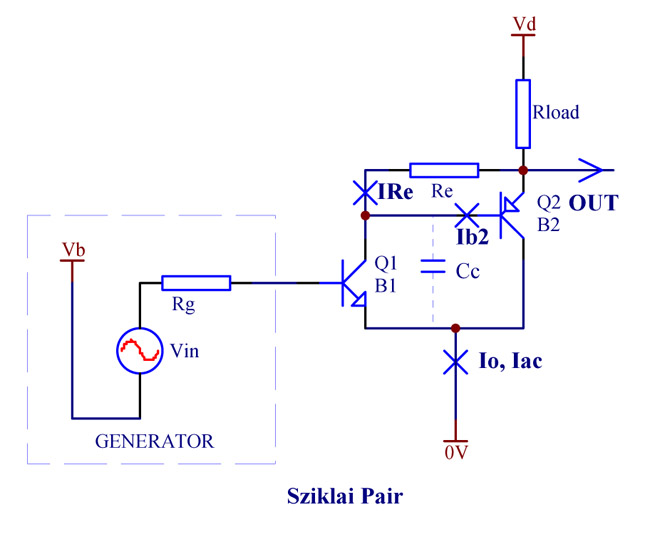
Fig. 2
Darlington and a Sziklai pair have much in common, but there are certain differences, especially if a resistor Re is used for shunting the emitter junction of the second transistor Q2. The following discussion helps understand how Re affects the performance of the two circuits. The following legend is used:
Io -- quiescent (DC) current;
Iac -- amplitude of the AC current component;
B1, B2 -- current gains of Q1 and Q2 respectively;
Re -- resistor, shunting the emitter junction of Q2;
Rg -- output signal source impedance;
IRe -- DC currents through Re;
Ib2 -- Q2 base DC current;
Cc -- Q2 collector junction barrier capacitance.
1. Reasonable range of Re
Reduction of Re causes the DC component through Q1 to rise, which in turn results in:
- transconductance (voltage gain) increase;
- input resistance reduction;
- slew rate and bandwidth increase;
- distortion reduction.
The smaller the Re, the greater are the above listed effects, but only to a certain point. Once Re becomes low enough and equal to the input resistance of Q2, further reduction of Re results in the total current gain loss and defeats the purpose of the Darlington. Thus, minimum reasonable Re is:
Remin = B2 * 0.025V / Io (1)
Before analyzing the effect of Re on the Darlington / Sziklai pair performance, it is convenient to introduce a "shunting factor" Ks, which is a ratio of the current through Re to the Q2 base current Ib2 .
Ks = IRe / Ib2 (2)
or
Ks = ( Vb * B2 ) / (Re * Io ) (3)
Here Vb is a typical voltage drop of a p-n junction. For silicon Vb = 0.6V.
The lower the Re, obviously the larger is the respective shunting factor Ks. The minimum reasonable Re (from (1)) corresponds to the maximum reasonable shunting factor
Ksmax = Vb / 0.025V = 0.6V / 0.025V = 24.
Making IRe more than 24 times greater than Ib2 serves no purpose.
For the same reasons, Ks shall be significantly smaller than B2. Further reduction of Re steers too much current away from Q2 base and is gradually turning a Darlington / Sziklai pair more and more into a single transistor Q1. With insufficient current through Q2, the later might enter AB class operation, which is not desirable. Eventually when Re = 0, transistor Q2 gets completely disabled.
Thus:
Ks < 24 (4)
In practice Ks < 10...15. (4a)
and/or
Ks << B2 (5),
whichever (4) or (5) dominates.
For high beta Q2, equation (4) prevails, for low beta Q2 -- (5) will have precedence. For practical purposes, "much less" sign in (5) means something about "less than 30...50% of". So:
Ks < (0.3...0.5) * B2 (5a)
2. Current gain
Current gain of a Darlington is B1*(B2+1) + B2. Current gain of a Sziklai pair is B1*(B2+1). This difference is immaterial, and it is common to assume that the compound beta B = B1 * B2. The compound beta is almost independent of the shunting resistor Re, if the shunting resistor is above its reasonable minimum, in other words, if Ks << 24.
3. Transconductance and input resistance
Without Re, a Darlington has only 50% of the transconductance of a virtual super-beta single equivalent transistor. Here and below we will be often comparing a Darlington / Sziklai pair to this reference transistor with virtual B = B1 * B2. Consequently, input resistance is twice that of the equivalent transistor. This is because voltage gain of Q1 is about 0.5:
SD = 0.5 * Io / 0.025V ZDin = 2* B1 * B2 * 0.025V / Io (6)
Transconductance and input resistance of a Sziklai pair exactly correspond to these of an equivalent reference transistor:
SZ = Io / 0.025V ; ZZin = B1 * B2 * 0.025V / Io (7)
Adding the shunting resistor Re or in other words, increasing shunting factor Ks leads to the transconductance rising and input resistance falling. For a classic Darlington (Fig. 1) these changes are insignificant, even for quite small Re -- about 1.5...1.9 times, making the Darlington look almost exactly like a reference transistor (5), while for a Sziklai pair the change can be large:
SZ = ( Io / 0.025V ) * (Ks + 1) ; ZZin = ( 0.025V / Io ) * (B1 * B2) / (Ks + 1) (8)
For that reason a Sziklai pair is preferred for amplification of small signals from a relatively low impedance source. Higher achievable transconductance of a Sziklai pair makes it useful as a low output impedance composite emitter follower. Apart from a popular application in the output stages of audio amplifiers, it is also useful in a simple voltage regulator with the following structure: Zener diode - RC noise filter - Sziklai pair.
Note that the equations are rather crude and assume Ks < 24, as was mentioned earlier.
4. Slew rate and output capacitance
To allow for fast transitions of the output signal, enough current shall be available to charge and discharge the collector capacitance Cc of Q2. For the negative output transitions, the discharging current available through Q1 is virtually unlimited, but for the positive transitions supply of the charging current is limited. Without Re, only Ib2 is available.
Slew rate = Io / (B2 * Cc). (9)
For example, with Io = 1mA, B2 = 200, Cc = 10pF, slew rate is 0.5V/µs, which is not great even for audio applications. Note that the slew rate limitation applies not only in a common emitter usage of the Darlington / Sziklai, but also to a common collector and common base. This should be kept in mind if a Darlington / Sziklai is to be used as booster follower in a "bootstrapped" gain stage (µ-follower) or as constant current source.
Reduction of Re increases supply of the charging current and proportionally facilitates the slew rate:
Slew rate = (Ks + 1) * Io / (B2 * Cc). (10)
Equations (9) and (10) apply to both Darlington and Sziklai pair, but for a Sziklai pair collector capacitances of Q1 and Q2 must be added together. Thus dynamic performance of a Sziklai pair is inferior compared to a classic Darlington.
In a Sziklai pair, junction capacitance Cc (Cc = Cc1 + Cc2) multiplied by B2 results in a hefty equivalent output capacitance present across "emitter" and "collector" of a Sziklai pair. For example, if Cc = 15pF and B2 = 100, output capacitance will equal to Cout = 1500pF. If such a Sziklai pair is used as an emitter follower, it is usually not a problem because of the low output impedance of such composite emitter follower. If the Sziklai pair is used in a common "base" configuration, for example, in a constant current source, then it is no problem either since the capacitive current is almost completely "recycled" from the collector back into the emitter.
However, if the Sziklai pair is used as a common emitter gain stage, this output capacitance might become a bandwidth limiting factor, depending on Rload.
Unfortunately for a Sziklai pair Cout is not affected by reduction of Re.
But things are much better for a Darlindton -- reduction of Re reduces the output capacitance. Besides, Cout is two times smaller for a start and does not include Q1:
Cout = Cc * B2 / (Ks + 2) (11)
Note that in any case, if a wider bandwidth and/or higher slew rate is required, it is reasonable to choose Q2 with a lower beta.
5. Distortion
Without Re, a Darlington (Fig. 1) or a Sziklai pair (Fig. 2) is as dreadful in terms of distortion as a single transistor. Perhaps even worse, as beta dependence on current of the two transistors is compounded. However, for simplicity we will assume constant betas for both transistors Q1 and Q2.
Without Re, for both both Darlington and Sziklai pair, in a common emitter configuration, distortion D equals:
D = ½ * (Iac / Io) (12)
This crude equation (12) takes only the second harmonic into account. Due to the exponential transfer function of a transistor the distortion depends only on the relative amount of AC component of the collector current. For example, if someone decides to make a single-ended class A power stage with say Io = 50mA quiescent current, swinging from 25mA to 75mA with signal applied, the distortion will be 25%, though only 60mV of drive will be needed on the input (30mV for Sziklai pair).
An attempt to drive fully from 0mA to 100mA will result in 50% of distortion or so. Needless to say, transistors without feedback are not suitable for linear amplification.
When Re is connected, the DC current through Q1 will increase, and the relative magnitude of AC component in the Q1 total current will reduce. Thus, voltage distortion in Q1 will drop. However, since in a Darlington (Fig. 1) both emitter junctions are connected in series, contribution of Q2 distortion will not change. So the gain will increase about 1.5...1.9 times, as has been mentioned earlier, the drive voltage will have to decrease in the same proportion and the distortion voltage referred to input will decrease in the same proportion, rendering the distortion unchanged.
Therefore in a Darlington (Fig. 1), distortion is not affected by Re.
In contrast to a Darlington, Sziklai pair (Fig. 2) responds to Re reduction quite well. For the analysis, the distortion of the Sziklai pair can be split into three components:
a) D1 -- voltage distortion in Q1, which reduces with the reduction of Re and consequent increase of DC current through Q1:
D1 = ½ * (Iac / Io) * (1 / (Ks + 1)) (13)
b) D2 -- voltage distortion in Q2, referred to input, which increases with the reduction of Re, because transconductance is rising while the distortion voltage reflected to input remains constant::
D2 = ½ * (Iac / Io) * (0.025V * Ks / Vb) (14)
or with Vb = 0.6V :
D2 = ½ * (Iac / Io) * (Ks / 24) (14a)
(Note again the same constant "24", related to the properties of silicon, as in (4)).
c) D3 -- distortion in Q2, reflected to input as current and producing distortion in the signal source ("GENERATOR") output impedance Rg. Obviously, it is proportional to Rg and rises quadratically with Re reduction:
D3 = ½ * (Iac / Io) * (Ks2 * Rg * Io ) / (B1 * B2 * Vb) (15)
In the equation (15), "Io" is not cancelled out deliberately, so that the first multiplicand " ½ * (Iac / Io) ", representing distortion of a single transistor, remains the same.
Very roughly:
D3 / D2 = Rg / ZZin , (16)
where ZZin -- input impedance of the Sziklai pair (8).
So the recipe for keeping input current distortion component D3 at bay is simple and obvious: keep the source impedance Rg lower than input impedance of the Sziklai pair.
A plot in Fig. 3 illustrated how all the three components of distortion and the total distortion Dtot depend on the shunting factor, that is on Re. The following conditions are used: Io = 1mA, Iac = 0.5mA, B1 = 50, B2 = 200, Rg = 15K.
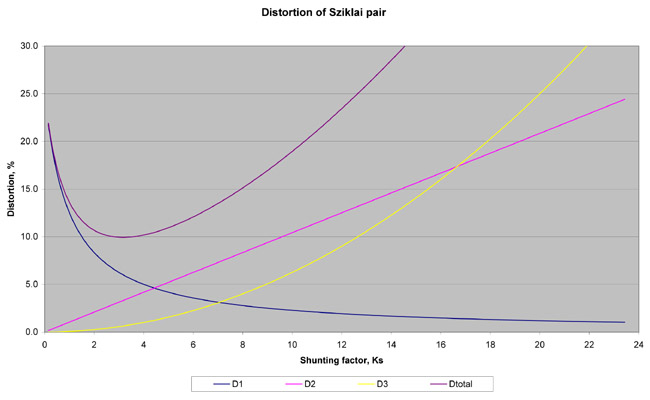
Fig. 3
in this case, a Sziklai pair can achieve about 2.2 times less distortion than a reference transistor or a classic Darlington (Fig. 1). The total distortion minimum is reached at about Ks = 3.5, in other words -- when the current through Re is 3.5 times larger than the Q2 base current.
6. Normalized distortion
Distortion figure in itself is not always the best characteristic of potential linearity of an amplifier. For instance, consider two amplifiers. One has gain of 10 and THD of 1%, while the other one -- gain of 100 and THD of 3%. Which one is more linear? The first one? Not necessarily. If we take the second amplifier and apply a negative feedback to reduce its excessive gain down to 10, its distortion will be reduced to 0.3%.
Thus, in order to compare potential linearity of some gain stages, one needs to fairly normalise the test results: normalise per unity gain, per unity transconductance, per unity output power (square root of), etc.
When dealing with a Darlington or a Sziklai pair, which is in effect a composite transistor-looking device, it is reasonable to normalise to the virtual reference super-beta equivalent single transistor with beta = B1 * B2 and the same quiescent current Io.
Suppose we are reducing Re (increasing Ks) in the Sziklai pair. Transconductance will increase beyond that of the reference transistor. Then we introduce a transconductance degenerating resistor (unbypassed "emitter" resistor) to bring the transconductance back to what the reference transistor would have had. This trick also brings the input resistance of the Sziklai pair back in line with the reference transistor. But now distortion of the Sziklai pair is reduced because of the negative feedback through the added emitter resistor. Thus we have exchanged the excessive transconductance for lower distortion. As a result, the Sziklai pair turned out a more linear device than a single super-beta reference transistor.
The plot below (Fig. 4) shows how Re reduction (Ks increase) in a Sziklai pair brings down the normalised distortion.
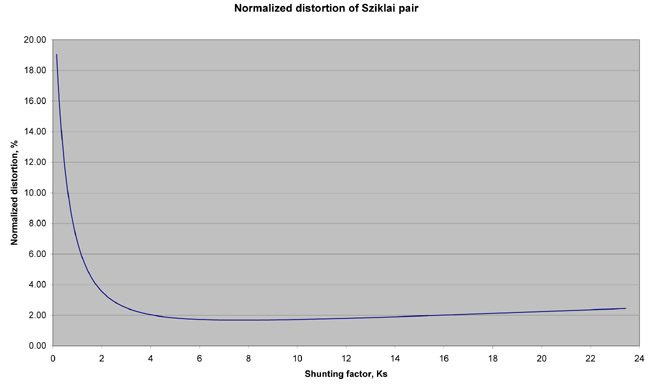
Fig. 4
Ideally, with Rg = 0 the lower is the Re -- the lower is the normalized distortion. It can be about 20 times less than of a reference transistor. In practice however, the rising current distortion component (D3) associated with Rg, prevents the normalized distortion from decreasing monotonically. Beyond a certain point, which is Ks = 7.5 under the above conditions, the distortion begins to slowly rise. Yet the normalised distortion reduction is quite marked -- from 25% to about 2%.
7. Conclusion
A Darlington (Fig. 1) and a composite Darlington (Sziklai pair) (Fig. 2) are the common techniques for creating a device similar to a super-beta transistor. Without a resistor Re shunting the emitter junction of the second transistor of the pair, and at low frequencies, Sziklai pair is almost identical in performance to an equivalent super-beta transistor, while a Darlington has 50% of transconductance and double the input impedance.
Dynamic performance of the Darlington / Sziklai pair is inferior to that of a reference transistor -- slew rate is limited and hefty output capacitance appears across "emitter - collector" terminals of the composite devices.
Introduction of Re modifies performance of the Darlington and Sziklai pair. When selecting Re value, DC current through Re shall not exceed 15...20 times the base current of the second transistor of the pair, even if beta of the second transistor is high.
Adding Re greatly increases slew rate and reduces output capacitance of the classic Darlington (Fig. 1), while for a Sziklai pair (Fig. 2) affects only the slew rate.
As far as distortion is concerned, Re has no effect on a Darlington, but can drastically reduce distortion and improve potential linearity of a Sziklai pair.
Transconductance can be exchanged for linearity. For example, a Darlington with a quiescent current of 50mA, driven from 5mA to 95mA would have 50% of THD, but it will have very high transconductance about 2000mA/V (quiescent). Connecting an unbypassed resistor in series with the "emitter" of the Darlington, one can lower its transconductance and increase linearity in the same proportion due to the negative feedback.
In this example, degenerating the transconductance from 2000mA/V to 5mA/V (by a 200 Ohm resistor) will result in THD of 0.13%. This THD is far lower than that of a vacuum tube, say 6V6GT, with the comparable transconductance.
This technique opens up an opportunity of creating Darlington vacuum tube replacements with lower distortion. Sziklai pair would give even better results with a lower Re, but high-voltage high power PNP transistors are not readily available.
